Breadcrumbs

About

introduction

Rainbows

Developed by E. Behringer

Easy JavaScript Simulation by Fremont Teng and Loo Kang Wee

This set of exercises guides the student in exploring primary and secondary rainbows. It requires the student to generate, observe, and describe plots of the deflection angles for light of different wavelengths and identify rainbow angles for different values of the relative index of refraction.

Subject Area	Waves & Optics
Levels	First Year and Beyond the First Year
Available Implementation	Python & Easy JavaScript Simulation
Learning Objectives	Students who complete this set of exercises will be able to obtain and use information from peer-reviewed literature. Plot an equation over a range of values. Analyze and compare plots (Exercises 1 and 2); write the deflection angle in terms of the relative index of refraction to calculate the deflection angle of rays entering spherical drops (Exercises 3 and 4); produce and describe graphs of deflection angle versus incident angle for light of different wavelengths (Exercises 3 and 4). identify rainbow angles for light of different wavelengths (Exercises 3 and 4); and crudely estimate the intensity as a function of detection angle (Exercise 5).
Time to Complete	120 min

1instructorguide

This set of exercises may be used in an introductory course that covers optics or in an upper-level optics course. The first three computational exercises are not demanding, but collectively provide an opportunity to deduce physical consequences (e.g., why is it that the primary and secondary rainbows are bright in particular directions). The last exercise is intended purely as a crude, ‘zeroeth order’ estimate of the irradiance as a function of deflection angle, purposefully neglecting polarization effects. Additional computational exercises have been described by D.S. Amundsen et al., Am. J. Phys. 77 (9), 795-798 (2009). An experimental apparatus to explore rainbows up to the 6th order has been described by G. Casini and A. Covello, Am. J. Phys. 80 (11), 1027-1034 (2012).

2theory

For Exercises 3 and 4, the theoretical concepts required are the Law of Refraction and the Law of Reflection, which are standard topics in introductory courses and are usually revisited in intermediate or advanced optics courses.

For Exercise 5, the crude model is nothing more than summing the irradiances associated with different rays, which implicitly assumes that the rays are incoherent with one another. Depending on the course, this can be contrasted with the ideas underlying the derivation of far field diffraction patterns - namely, that one works with the electric fields and carefully accounts for the relative phases of contributions from different parts of an extended source.

Exercise 1

EXERCISE 1: OBTAIN AND USE INFORMATION FROM PEER-REVIEWED LITERATURE

Water and air are the two materials involved with producing rainbows we may see in the sky after a thunderstorm. To accurately predict where rainbows will appear, we need to have accurate information about the refractive indices of water and air.

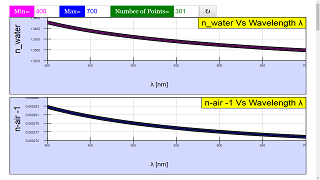
(a) Obtain a copy of “Models for the wavelength dependence of the index of refraction of water”, Applied Optics 36 (16), 3785-3787 (1997) by Paul D.T. Huibers, and use Eq. (3) of that paper to generate a plot of the refractive index of water as a function of wavelength in the range from 400 to 650 nm.

(b) Obtain a copy of “Refractive index of air: new equations for the visible and near infrared”, Applied Optics 35(9), 1566-1573 (1996) by Philip E. Ciddor, and use Eq. (1) of that paper to generate a plot of , the deviation of the refractive index of air from unity, as a function of wavelength in the range from 400 to 650 nm.

Which material has the larger change in refractive index over the wavelength range from 400 to 650 nm? Calculate the ratio of the larger change to the refractive index of the material for a wavelength of 400 nm, and comment on the magnitude of the ratio.

3exercises

EXERCISE 1: OBTAIN AND USE INFORMATION FROM PEER-REVIEWED LITERATURE

(b) Obtain a copy of “Refractive index of air: new equations for the visible and near infrared”, Applied Optics 35(9), 1566-1573 (1996) by Philip E. Ciddor, and use Eq. (1) of that paper to generate a plot of $n_{a i r} - 1$ , the deviation of the refractive index of air from unity, as a function of wavelength in the range from 400 to 650 nm.

EXERCISE 2: DEFLECTION ANGLE FOR A LIGHT RAY ENTERING A SPHERICAL RAINDROP

Assume that a light ray incident on a spherical raindrop at an angle $θ_{1 i}$ measured with respect to the surface normal undergoes one internal reflection before leaving the raindrop, as shown below.

Alt Figure: Geometry of a ray incident on a spherical raindrop. `

Show that if $θ_{i} \equiv θ_{1 i}$ and $θ_{r} \equiv θ_{1 t}$ , then the deflection angle $δ$ of the light ray is (in radians):

\begin{matrix} (1) & δ = 2 (θ_{i} - θ_{r}) + (π - 2 θ_{r}) \end{matrix}

The deflection angle $δ$ is the angle between the incident ray and the outgoing ray, and $θ_{r}$ is the angle of refraction for the light ray incident from air and entering water. To compute the deflection angle, what quantities must be known?

EXERCISE 3: COMPUTE THE DEFLECTION ANGLE VERSUS INCIDENT ANGLE

Generate a plot of the deflection angle $δ$ as a function of incident angle $θ_{i}$ for light rays of wavelength 400 nm that experience one internal reflection in the raindrop. Compare, on the same plot, the deflection angle for light rays of wavelength 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the rainbow? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

Near the minimum of the deflection function (that is, the $δ (θ_{i})$ curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observer, what is implied by your answer?

EXERCISE 4: WHERE IS THE SECONDARY (DOUBLE) RAINBOW?

Repeat the computation of Exercise 3, but now assume that the ray undergoes two internal reflections within the raindrop. In this case, show that the deflection angle is given by

\begin{matrix} (2) & δ = 2 (θ_{i} - θ_{r}) + 2 (π - 2 θ_{r}) \end{matrix}

and plot the deflection angle versus the incident angle for rays of wavelength 400 nm and 650 nm. The two curves should have minima that are close to each other, but not identical. What are the values of the incident angle corresponding to these two minima? Assuming that these minima correspond to the rainbow direction, what direction do you have to look relative to the horizontal to see the bright red band of the secondary rainbow? Can a ground based observer see these rays? Do the rays that produce the secondary rainbow enter the top of the raindrop? What direction do you have to look relative to the horizontal to see the bright violet band? Which band appears higher in the sky?

EXERCISE 5: CRUDE ESTIMATE OF THE IRRADIANCE VERSUS DEFLECTION ANGLE FOR A SINGLE WAVELENGTH: PRIMARY RAINBOW

Assume that the each outgoing ray produces an irradiance that is equal to $I (θ) = I_{0} \exp [- (θ - δ)^{2}]$ where here the angles are assumed to be in degrees and the implied width of this distribution is $1^{\circ}$ . (For simplicity, we neglect the loss of intensity during refraction and internal reflection. This is a huge oversimplification, but it allows us to focus on adding up contributions from each ray.) Sum up the contributions from rays uniformly distributed over the scaled impact parameter $\tilde{b} = b / R$ to compute the overall irradiance as a function of deflection angle for light of wavelength 400 nm. Plot the resulting irradiance distribution versus deflection angle for a single wavelength. How does this plot help explain why the rainbow is bright?

Code Rainbows_Exercise_1.py

# Rainbows_Exercise_1.py

# Plot separately the refractive indices of

# water and air, based on peer-reviewed literature

# The refractive index of water is taken from

# Eq. 3 of P.D.T Huibers, Applied Optics,

# Vol. 36, No. 16, pp. 3785-3787 (1997).

# The refractive index of air is taken from

# Eq. 1 of P.E. Ciddor, Applied Optics,

# Vol. 35, No. 9, pp. 1566-1573 (1996).

# Written by:

# Ernest R. Behringer

# Department of Physics and Astronomy

# Eastern Michigan University

# Ypsilanti, MI 48197

# (734) 487-8799

# This email address is being protected from spambots. You need JavaScript enabled to view it.

# 20160109 by ERB add plots of index versus wavelength

from pylab import figure,plot,xlim,xlabel,ylim,ylabel,grid,title,show

from numpy import linspace

# Define the index of refraction function for water

def water_index(wavelength):

n_H2O = 1.31279 + 15.762/wavelength - 4382.0/(wavelength**2) + 1.1455e6/(wavelength**3)

return(n_H2O)

# Define the index of refraction function for air

# Note: wavelength is supposed to be in micrometers

def air_index_minus_one(wavelength):

term1 = 0.05792105/(238.0185 - 1.0e6/(wavelength**2))

term2 = 0.00167917/(57.362 - 1.0e6/(wavelength**2))

return(term1+term2)

# Inputs

lambda_lo = 400.0 # low value of the wavelength [nm]

lambda_hi = 700.0 # high value of the wavelength [nm]

npts = 301 # number of points for the array of wavelengths

# Generate the array of wavelengths

wavelengths = linspace(lambda_lo,lambda_hi,npts)

# Calculate the refractive indices

n_water = water_index(wavelengths)

n_air = 1.0 + air_index_minus_one(wavelengths)

#----------------------------------------------------------------------

# Start a new figure. This will be a plot of

# refractive index of water versus wavelength.

figure()

# Set the limits of the horizontal axis

xlim(lambda_lo,lambda_hi)

# Label the horizontal axis

xlabel("$\\lambda$ [nm]", size = 16)

# Set the limits of the vertical axis

ylim(1.325,1.345)

# Label the vertical axis

ylabel("$n_{water}$", size = 16)

# Draw a grid

grid(True)

# Make the title

title("$n_{water}$ versus wavelength $\\lambda$\n Appl. Opt. Vol. 36, Pg. 3785 (1997)")

# Plot the refractive index of water versus wavelength

plot(wavelengths,n_water,"m-")

show()

#----------------------------------------------------------------------

# Start a new figure. This will be a plot of

# refractive index of air versus wavelength.

figure()

# Set the limits of the horizontal axis

xlim(lambda_lo,lambda_hi)

# Label the horizontal axis

xlabel("$\\lambda$ [nm]", size = 16)

# Set the limits of the vertical axis

ylim(2.75e-4,2.85e-4)

# Label the vertical axis

ylabel("$n_{air} - 1$", size = 16)

# Draw a grid

grid(True)

# Make the title

title("$n_{air} - 1$ versus wavelength $\lambda$\n Appl. Opt. Vol. 35, Pg. 1566 (1996)")

# Plot the refractive index of air minus one

plot(wavelengths,air_index_minus_one(wavelengths),"m-")

show()

4solutions

Exercise 1: Obtain and use information from peer-reviewed literature

The plot for the refractive index of water should look like:

Alt Figure: Geometry of a ray incident on a spherical raindrop. `

The plot for the deviation of the refractive index of air from unity should look like:

Alt Figure: Geometry of a ray incident on a spherical raindrop.

Exercise 2: Deflection angle for a light ray entering a spherical raindrop

To calculate the deflection angle, one needs to know the refractive index of the air and the water at the particular wavelength and also the angle of incidence of the incoming ray. The laws of refraction and reflection are then applied to obtain the angles of refraction and the angle of reflection for the internal reflection. Students should be able to show that the equalities shown in the figure illustrating the ray/raindrop geometry.

Exercise 3: Compute the deflection angle versus incident angle

The solution for Exercise 3 is:

Alt Figure: Geometry of a ray incident on a spherical raindrop.

The minimum of the deflection function for $λ = 400$ nm ( $λ = 650$ nm) is $δ = {139.3}^{\circ}$ $(δ = {137.6}^{\circ})$ . This means that you must look (with the sun at your back and the distant raindrops in front of you) at an angle of $180^{\circ} - {139.3}^{\circ} = {40.7}^{\circ}$ $(180^{\circ} - {137.6}^{\circ} = {42.4}^{\circ})$ relative to the horizontal to see the bright violet (red) band of the rainbow. So the red band appears above the violet band. (It really does!) It is worth noting that the rays producing the primary rainbow enter the top half of the raindrops.

Exercise 4: Where is the double (secondary) rainbow?

The solution for Exercise 4 is: Alt Figure: Geometry of a ray incident on a spherical raindrop.

The minimum of the deflection function for $λ = 400$ nm ( $λ = 650$ nm) is $δ = {233.3}^{\circ}$ ( $δ = {230.2}^{\circ}$ ). These rays are directed back up into the sky and the ground-based observer wonâ€™t see them. However, if you realize that you have just computed the deflection angles for rays entering the bottom half of the raindrop, you realize that you must look (with the sun at your back and the distant raindrops in front of you) at an angle of ${233.3}^{\circ} - 180^{\circ} = {53.3}^{\circ},, ({230.2}^{\circ} - 180^{\circ} = {50.2}^{\circ})$ relative to the horizontal to see the bright violet (red) band of the rainbow. So the red band of the secondary rainbow appears below the violet band. (It really does!). Thus the rays producing the secondary rainbow enter the bottom half of the raindrops and the order of the color bands is reversed relative to the primary rainbow. Comparing these angles to those from Exercise 3, we see that the secondary rainbow appears above the primary rainbow. The reduced brightness of the secondary rainbow is due to the additional internal reflection and the corresponding loss of irradiance during that reflection. It is posible to extend Exercises 3 and 4 to account for the change in intensity occurring for every refraction or internal reflection. For fun, it must be noted that fascination with the double rainbow became an Internet meme in 2010 when a person living on the border of Yosemite National Park recorded his reaction to a spectacular double rainbow. At the time of writing, the video can be seen at: https://www.youtube.com/watch?v=OQSNhk5ICTI).

Exercise 5: Crude estimate of the irradiance versus deflection angle for a single wavelength: Primary Rainbow

The solution for Exercise 5 is: Alt Figure: Geometry of a ray incident on a spherical raindrop.

Note that irradiance is distributed over a large range of detection angles, and that the irradiance has a peak near (but not at) the minimum of the deflection function for these chosen parameters. If we use an angular width smaller than $1^{\circ}$ for the assumed irradiance distribution of a ray, the irradiance peak approaches the minimum in the deflection angle and the “background irradiance” decreases. The main result is that irradiance accumulates in the direction specified by the minimum in the deflection function because several rays are deflected into essentially the same direction. This is known as rainbow scattering, and it is also observed in scattering events such as atomic/molecular collisions or ion collisions with ordered surfaces.

5references

Most introductory textbooks mention rainbows and the angles at which they can be observed, but do not necessarily explain why rainbows are bright. This set of exercises is intended to show how irradiance “piles up” around the minima of the deflection functions calculated in Exercises 3 and 4.

Translations

Code	Language		Translator	Run

Credits

Fremont Teng; Loo Kang Wee; based on Ernest R. Behringer python code

Overview:

This document provides a review of the "PICUP Refractive Indices of Water and Air JavaScript Simulation Applet HTML5" resource. This resource offers a set of exercises designed to guide students in understanding the formation of primary and secondary rainbows. It utilizes computational tasks and analysis of peer-reviewed literature to explore the relationship between the refractive indices of water and air, the deflection of light through raindrops, and the resulting visual phenomenon of rainbows. The exercises are suitable for introductory and upper-level optics courses.

Main Themes and Important Ideas/Facts:

Refractive Indices of Water and Air are Wavelength Dependent: The initial exercises (Exercise 1) focus on obtaining and utilizing data from peer-reviewed publications to understand how the refractive indices of water and air vary with the wavelength of light. Students are required to:

Obtain the paper "Models for the wavelength dependence of the index of refraction of water" by Paul D.T. Huibers and plot the refractive index of water as a function of wavelength (400-650 nm) using Equation (3) from the paper.
Obtain the paper "Refractive index of air: new equations for the visible and near infrared" by Philip E. Ciddor and plot the deviation of the refractive index of air from unity (n_air - 1) as a function of wavelength (400-650 nm) using Equation (1) from the paper.
Compare the change in refractive index for both materials over the specified wavelength range and comment on the magnitude of the ratio of the larger change to the refractive index at 400 nm.

This exercise emphasizes the fundamental role of wavelength-dependent refractive indices in the dispersion of light, which is crucial for the formation of rainbows. It also introduces students to using real scientific literature and performing basic data analysis.
Deflection Angle of Light Rays in Raindrops: Exercises 2, 3, and 4 delve into the geometry of light rays passing through spherical raindrops, focusing on the concept of the deflection angle.

Exercise 2: Derives the formula for the deflection angle ($\delta$) of a light ray undergoing one internal reflection within a raindrop:
$\delta = 2 ( \theta i − \theta r ) + ( \pi − 2 \theta r )$ where $\theta_i$ is the angle of incidence and $\theta_r$ is the angle of refraction. The exercise prompts students to identify the necessary quantities to compute this angle (refractive indices of air and water at the specific wavelength, and the angle of incidence). This reinforces the application of the Law of Refraction and the Law of Reflection.
Exercise 3: Requires students to plot the deflection angle as a function of the incident angle for wavelengths of 400 nm (violet) and 650 nm (red), assuming one internal reflection (primary rainbow). They are asked to identify the minima of these curves, which correspond to the rainbow angles for each color, and to determine the apparent position of the red and violet bands in the sky relative to the horizontal. The solution reveals that the minimum deflection angles for violet and red light are approximately 139.3° and 137.6° respectively, leading to viewing angles of 40.7° (violet) and 42.4° (red) above the horizontal, with red appearing higher. This explains the color order of the primary rainbow.
Exercise 4: Repeats the process for two internal reflections (secondary rainbow), with a modified deflection angle formula:
$\delta = 2 ( \theta i − \theta r ) + 2 ( \pi − 2 \theta r )$ Students plot the deflection angle for 400 nm and 650 nm light and identify the minima. The solution indicates minimum deflection angles of 233.3° (violet) and 230.2° (red). Considering that these rays enter the bottom of the raindrop, the viewing angles are 53.3° (violet) and 50.2° (red) above the horizontal, with red appearing below violet. This explains the reversed color order of the secondary rainbow, which appears above the primary rainbow due to the larger viewing angles. The text also notes the reduced brightness of the secondary rainbow due to the additional reflection.

Rainbow Angles and Brightness: The exercises highlight that rainbows are observed at specific angles corresponding to the minima in the deflection angle functions. The text explains: "Near the minimum of the deflection function (that is, the $\delta(\theta_i)$ curve), are two rays with slightly different incident angles deflected into different directions? Regarding the brightness of the deflected light perceived by an observer, what is implied by your answer?" The answer implicitly suggests that near the minimum, many rays with slightly different incident angles are deflected into nearly the same direction, leading to a higher intensity of light observed at these angles. This is the fundamental reason why rainbows appear as bright arcs.
Crude Estimate of Irradiance: Exercise 5 attempts to provide a basic understanding of the brightness of the primary rainbow by modeling the irradiance of each outgoing ray as a Gaussian function centered at the deflection angle. Students are asked to sum the contributions from rays with uniformly distributed impact parameters to obtain the overall irradiance as a function of deflection angle for a single wavelength (400 nm). The solution states: "The main result is that irradiance accumulates in the direction specified by the minimum in the deflection function because several rays are deflected into essentially the same direction. This is known as rainbow scattering". This exercise, while simplified by neglecting intensity losses and polarization, demonstrates the concept of enhanced brightness at the rainbow angle due to the concentration of deflected light.

Learning Objectives:

The exercises aim to enable students to:

"obtain and use information from peer-reviewed literature. Plot an equation over a range of values. Analyze and compare plots (Exercises 1 and 2);"
"write the deflection angle in terms of the relative index of refraction to calculate the deflection angle of rays entering spherical drops (Exercises 3 and 4);"
"produce and describe graphs of deflection angle versus incident angle for light of different wavelengths (Exercises 3 and 4)."
"identify rainbow angles for light of different wavelengths (Exercises 3 and 4);"
"crudely estimate the intensity as a function of detection angle (Exercise 5)."

Target Audience:

The resource is intended for students in:

Introductory courses covering optics.
Upper-level optics courses.

Computational Tools:

The exercises require students to perform calculations and generate plots, suggesting the use of tools like:

Python (as indicated by the provided Rainbows_Exercise_1.py code, which plots refractive indices).
Easy JavaScript Simulation (EjsS), as the applet is built using this platform.

Instructor Guidance:

The instructor guide suggests that the exercises provide an opportunity to deduce why primary and secondary rainbows are bright in particular directions. It also mentions additional computational exercises in the American Journal of Physics.

Conclusion:

The "PICUP Refractive Indices of Water and Air JavaScript Simulation Applet HTML5" offers a comprehensive and engaging way for students to explore the physics behind rainbows. By combining the use of scientific literature, mathematical derivations, and computational analysis, it provides a deeper understanding of the role of refractive indices, light deflection, and the formation of these captivating optical phenomena. The exercises progressively build upon fundamental concepts of optics, culminating in a basic understanding of the intensity distribution that leads to the bright arcs we observe.

Study Guide: Rainbow Formation

Key Concepts

Refraction: The bending of light as it passes from one medium to another with a different refractive index. Governed by Snell's Law.
Refractive Index (n): A measure of how much the speed of light is reduced inside a medium compared to the speed of light in a vacuum. It is wavelength-dependent.
Dispersion: The phenomenon where the refractive index of a material varies with the wavelength (color) of light, causing different colors of light to bend at slightly different angles.
Reflection: The bouncing back of light when it strikes a surface. For internal reflection within a raindrop, the angle of incidence equals the angle of reflection.
Angle of Incidence (θᵢ): The angle between an incoming ray of light and the normal (a line perpendicular to the surface) at the point of incidence.
Angle of Refraction (θ<0xE1><0xB5><0xA7>): The angle between a refracted ray of light and the normal at the point of refraction.
Deflection Angle (δ): The angle between the incident ray of light and the outgoing ray of light after interacting with a raindrop.
Primary Rainbow: Formed by light undergoing one internal reflection inside a raindrop.
Secondary Rainbow: Formed by light undergoing two internal reflections inside a raindrop.
Rainbow Angle: The angle of observation relative to the direction opposite the sun at which the intensity of the rainbow is highest. This corresponds to the minimum deflection angle.
Irradiance: The power of electromagnetic radiation incident per unit area of a surface.

Quiz

What two phenomena are primarily responsible for the formation of rainbows in the sky after a thunderstorm? Briefly describe each phenomenon.
Explain the concept of refractive index and how it relates to the speed of light in a medium. How does the refractive index of water and air typically vary with the wavelength of visible light?
Describe the path of a light ray through a spherical raindrop that leads to the formation of a primary rainbow. How many internal reflections occur in this process?
How is the deflection angle of a light ray defined in the context of rainbow formation? What factors determine the magnitude of this angle for a ray incident on a raindrop?
What is the significance of the minimum deflection angle in the formation of a rainbow? How does this minimum angle relate to the angle at which a rainbow is observed?
Explain how dispersion within water droplets leads to the separation of sunlight into different colors in a rainbow. Which color of light is typically deflected at a smaller angle in a primary rainbow?
Describe the path of a light ray through a spherical raindrop that leads to the formation of a secondary rainbow. How does the number of internal reflections differ from that of a primary rainbow?
How does the order of colors in a secondary rainbow compare to the order of colors in a primary rainbow? Briefly explain the reason for this difference.
What is the crude model used to estimate the irradiance as a function of deflection angle for a primary rainbow? What key assumption does this model make?
Why is the rainbow observed as a bright arc in the sky rather than a uniformly illuminated area? Relate your answer to the concept of the minimum deflection angle.

Quiz Answer Key

The two primary phenomena responsible for rainbow formation are refraction and reflection. Refraction is the bending of light as it enters and exits the water droplets, while reflection is the bouncing of light off the back surface of the droplets.
The refractive index (n) is the ratio of the speed of light in a vacuum to the speed of light in a medium, indicating how much light slows down in that medium. Both water and air have refractive indices that are wavelength-dependent; typically, the refractive index is higher for shorter wavelengths (like violet) and lower for longer wavelengths (like red).
For a primary rainbow, a light ray enters the top half of a raindrop, refracts at the air-water interface, undergoes one internal reflection off the back of the droplet, and then refracts again as it exits. This process involves a single internal reflection.
The deflection angle is the angle between the incident direction of the sunlight and the direction of the light ray after it has interacted with the raindrop. This angle is determined by the refractive indices of air and water at the specific wavelength of light and the incident angle of the ray.
The minimum deflection angle corresponds to the direction where a large number of light rays emerge from the raindrops with very similar deflection angles. This "piling up" of light intensity at this angle is what creates the bright arc of the rainbow observed by a viewer.
Dispersion occurs because different wavelengths of light are refracted at slightly different angles when entering and exiting the water droplet due to the wavelength dependence of the refractive index. In a primary rainbow, violet light is deflected at a larger angle (around 40.7 degrees from the horizontal), while red light is deflected at a smaller angle (around 42.4 degrees from the horizontal), thus red appears higher.
For a secondary rainbow, a light ray enters the bottom half of a raindrop, refracts, undergoes two internal reflections off the back of the droplet, and then refracts again as it exits. This process involves two internal reflections.
The order of colors in a secondary rainbow is reversed compared to a primary rainbow, with red appearing on the inside and violet on the outside. This reversal occurs because of the two internal reflections, which cause a different relationship between wavelength and the final direction of the light.
The crude model estimates irradiance by summing the contributions from individual outgoing rays, assuming each ray produces a Gaussian distribution of irradiance centered around its deflection angle. This model simplifies the situation by neglecting the loss of intensity due to refraction and internal reflection and assumes incoherent rays.
The rainbow appears as a bright arc because the intensity of the deflected light is significantly higher near the minimum deflection angle. Many rays with slightly different incident angles are deflected into nearly the same direction around this minimum, leading to a concentration of light observed at a specific angle from the observer.

Essay Format Questions

Discuss the roles of refraction, reflection, and dispersion in the formation of both primary and secondary rainbows. Compare and contrast the light paths and the resulting visual characteristics of these two types of rainbows.
Explain the mathematical relationship between the incident angle, the angle of refraction, and the deflection angle for light rays interacting with spherical raindrops in the context of primary and secondary rainbow formation. How does the wavelength dependence of the refractive index influence these angles?
Analyze the concept of the minimum deflection angle and its importance in understanding the visibility and angular position of rainbows. How does the minimum deflection angle vary for different wavelengths of light, and what are the implications for the colors observed in a rainbow?
Critically evaluate the "crude estimate of irradiance" model for rainbow formation. What are its key assumptions and limitations? How does the piling up of irradiance near the minimum deflection angle contribute to the brightness of a rainbow?
Investigate the historical and scientific significance of understanding rainbow formation. How has the study of rainbows contributed to our understanding of optics, and what are some advanced phenomena related to rainbows beyond the primary and secondary bows?

Glossary of Key Terms

Law of Refraction (Snell's Law): States the relationship between the angles of incidence and refraction, and the refractive indices of the two media at an interface: n₁sin(θ₁) = n₂sin(θ₂).
Law of Reflection: States that when a ray of light reflects off a surface, the angle of incidence is equal to the angle of reflection, and the incident ray, the reflected ray, and the normal to the surface at the point of incidence all lie in the same plane.
Wavelength (λ): The spatial period of a periodic wave—the distance over which the wave's shape repeats. In the context of light, it determines the color.
Normal: A line perpendicular to a surface at a specific point. Angles of incidence and refraction are measured with respect to the normal.
Incident Ray: The ray of light that strikes a surface.
Refracted Ray: The ray of light that passes through a surface and bends due to a change in speed.
Reflected Ray: The ray of light that bounces back from a surface.
Spherical Drop: A raindrop, which is approximately spherical in shape.
Peer-Reviewed Literature: Scholarly works that have been examined and approved by experts in the same field before publication.
Plots: Visual representations of data, such as graphs showing the relationship between two or more variables.
Computational Exercises: Problems that require mathematical calculations, often involving plotting and analyzing data.
Relative Index of Refraction: The ratio of the refractive index of one medium to that of another.
Incident Angle (θ₁ᵢ): The angle at which a light ray strikes the outer surface of a raindrop, measured with respect to the normal.
Angle of Refraction (θ₁ₜ): The angle at which a light ray enters the raindrop, measured with respect to the normal.
Minimum of the Deflection Function: The smallest value of the deflection angle as a function of the incident angle, which corresponds to the brightest part of the rainbow.
Irradiance Distribution: How the intensity of light is spread out over different angles.
Scaled Impact Parameter (b̃ = b/R): The ratio of the impact parameter (the perpendicular distance from the center of the raindrop to the incident ray's path) to the radius of the raindrop (R).
Incoherent: Light waves that do not have a constant phase relationship, so their intensities simply add together.
Far Field Diffraction Patterns: Interference patterns observed at a large distance from an aperture or obstacle, where the phase differences between waves from different parts of the source are significant.
Rainbow Scattering: The phenomenon responsible for the brightness of rainbows, where light is preferentially scattered in directions corresponding to the extrema (minima or maxima) of the deflection angle.

Sample Learning Goals

[text]

For Teachers

Refractive Indices of Water and Air JavaScript Simulation Applet HTML5

Instructions

Control Panel

Editing the inputs in the field boxes will change their minimum/maximum and number of points respectively.

Toggling Full Screen

Double clicking anywhere in the panels will toggle full screen.

Reset Button

Resets the simulation.

Research

[text]

Video

[text]

Version:

Other Resources

[text]

Frequently Asked Questions on Rainbow Formation

What are the primary optical phenomena responsible for the creation of rainbows?

Rainbows are primarily formed through the refraction and reflection of sunlight within water droplets. As sunlight enters a spherical raindrop, it is first refracted (bent) at the air-water interface. The light then travels to the back of the raindrop, where it undergoes internal reflection. Finally, as the light exits the raindrop, it is refracted again.

Why do rainbows exhibit different colors, and in what order are they typically observed in a primary rainbow?

The separation of sunlight into its constituent colors occurs due to the phenomenon of dispersion during refraction. The refractive index of water varies slightly with the wavelength (and thus color) of light. Violet light has a slightly higher refractive index than red light, causing it to be bent more. In a primary rainbow, the colors are observed in the order of red on the outer arc, followed by orange, yellow, green, blue, indigo, and violet on the inner arc.

What is the deflection angle of light in a raindrop, and what factors determine its value?

The deflection angle is the angle between the incident ray of sunlight and the outgoing ray after interacting with the raindrop. For a light ray undergoing one internal reflection (as in a primary rainbow), the deflection angle (δ) is given by δ = 2(θᵢ - θ<0xE1><0xB5><0xA7>) + (π - 2θ<0xE1><0xB5><0xA7>), where θᵢ is the angle of incidence and θ<0xE1><0xB5><0xA7> is the angle of refraction. The deflection angle depends on the incident angle and the refractive index of water at the specific wavelength of light.

What is the significance of the minimum deflection angle in the context of rainbow formation?

The minimum in the deflection angle curve (when plotted against the incident angle) is crucial for the visibility and brightness of rainbows. Near this minimum angle, many parallel rays of sunlight incident on the raindrops at slightly different angles will be deflected into almost the same outgoing direction. This "piling up" of light rays at a specific angle leads to a higher intensity of light observed by an observer, creating the bright arc of the rainbow. This phenomenon is known as rainbow scattering.

How is a secondary (double) rainbow formed, and how does it differ from a primary rainbow in terms of internal reflections and color order?

A secondary rainbow is formed when sunlight undergoes two internal reflections within the raindrop before exiting. The deflection angle for a secondary rainbow is given by δ = 2(θᵢ - θ<0xE1><0xB5><0xA7>) + 2(π - 2θ<0xE1><0xB5><0xA7>). Due to the additional internal reflection, the order of colors in a secondary rainbow is reversed compared to the primary rainbow, with red on the inner arc and violet on the outer arc. The secondary rainbow is also typically fainter than the primary rainbow because of the additional light lost during the second internal reflection.

At what approximate angles relative to the horizontal are the primary and secondary rainbows typically observed?

The bright bands of the primary rainbow (corresponding to the minimum deflection angles) are observed at angles of approximately 40.7° (violet) to 42.4° (red) relative to the horizontal, with the sun at the observer's back. The secondary rainbow appears at a higher angle, approximately 50.2° (red) to 53.3° (violet) relative to the horizontal, and the order of colors is reversed.

Why are rainbows observed as arcs?

Rainbows appear as arcs because the condition for seeing the intensified light at the minimum deflection angle is met by raindrops that lie on a cone centered on the line extending from the sun to the observer's eye. Only the raindrops along the circumference of this cone will return the intensified, dispersed light to the observer, resulting in the arc shape.

How does the wavelength of light affect the refractive index of water and the resulting rainbow?

The refractive index of water is wavelength-dependent; it is higher for shorter wavelengths (violet light) and lower for longer wavelengths (red light). This variation in refractive index leads to different deflection angles for different colors of light. Consequently, the minima in the deflection angle curves for different wavelengths occur at slightly different angles of incidence, resulting in the angular separation of colors observed in a rainbow. For the primary rainbow, violet light is deflected more and appears at a smaller angle relative to the anti-solar point than red light.

1 1 1 1 1 1 1 1 1 1 Rating 0.00 (0 Votes)

Details: Written by Fremont; Parent Category: 03 Waves; Category: 04 Light; Published: 11 June 2018; Created: 11 June 2018; Last Updated: 22 March 2025; Hits: 4798

Light
PICUP